Bruchmechanik von Glas (Bauteilwiderstand)
Allgemeines
Hauptursache für die geringe Zugfestigkeit von Floatglas sind die Oberflächendefekte in Verbindung mit der fehlenden Zähigkeit des Materials. Die hohe Spannungsspitze an der Risswurzel kann nicht durch Plastifizierung abgebaut werden. Für eine Beschreibung des Spannungszustandes im Nahfeldbereich d des Risses liegt die Vorstellung einer unendlich ausgedehnt gedachten Scheibe unter konstanter Zugbelastung zugrunde. Die Modellvorstellung für die im Folgenden vorgestellte Bruchmechanik setzt zudem voraus, dass die Scheibendicke h wesentlich größer als die Risstiefe a ist und kräftefreie Rissflanken existieren. Nur unter diesen Festlegungen lassen sich die am Modell von GRIFFITH gefundenen Zusammenhänge sinnvoll auf die Oberflächenschädigungen anwenden.
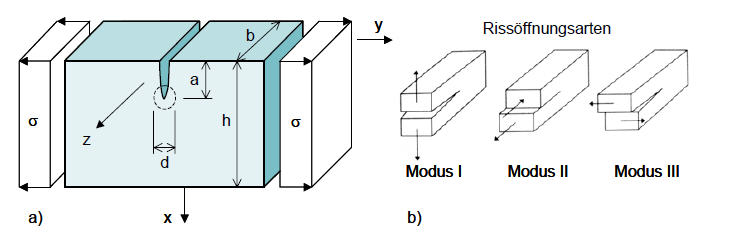
Abb. 1: a) Einzelriss unter Zugbelastung s, Nahfeldzone d, h >> a [1]; b) Rissöffnungsarten [2]
Wie in Abb. 1 b) zu sehen ist, werden in der Bruchmechanik verschiedene Rissöffnungsarten unterschieden. Modus I beschreibt eine Klaffung senkrecht zur Rissfläche, Modus II beschreibt eine Längsscherung und Modus III ist bei Querscherungen anzuwenden. Für den Glasbau ist in erster Linie Modus I entscheidend.
Festigkeit von nicht vorgespannten Glasprodukten in inerter (reaktionsunfähiger) Umgebung
Die theoretische Festigkeit von Glas lässt sich aus den atomaren Bindefestigkeiten ableiten. Hierbei spielt die spezifische Oberflächenenergie g0 (auch: Oberflächenspannung), welche eigentlich eine temperaturabhängige Größe für flüssige Zustände ist, eine entscheidende Rolle. Der feste Glaszustand wird häufig mit einer unterkühlten Flüssigkeit gleichgesetzt, die ohne zu kristallisieren erstarrt ist [1, Abschnitt 4.1.1]. Dementsprechend erfolgt die übliche Bestimmung der spezifischen Oberflächenenergie in der zähflüssigen Phase (z.B. Abreiß- oder Lamellenmethode), wobei mit sinkender Temperatur ein leichter Anstieg dieses Materialwertes zu verzeichnen ist. Anschließend wird durch Extrapolation auf Raumtemperatur der Rechenwert für den festen Zustand abgeleitet. Es existieren durch die Methode und die jeweilige Glaszusammensetzung Streuungen der Ergebnisse, wobei meist auf der sicheren Seite liegende untere Grenzwerte in Veröffentlichungen zu finden sind, so dass die Genauigkeit der theoretischen Ergebnisse von vornherein eingeschränkt ist.
Gl. 1
![]()
mit:
sth … theoretische Zugfestigkeit von Glas ohne Oberflächendefekte,
E … E-Modul von Glas (≈ 70000 MN/m²),
g0 … spezif. Oberflächenenergie (3,0 ∙ 10-6 … 5,4 ∙ 10-6 MN/m, [3] [4]),
d0 … Ionenabstand Si-O (≈ 2 ∙ 10-10 m, [3])
Die in der Baubranche üblichen Natron-Kalk-Silicatgläser enthalten neben Siliziumoxiden noch andere Komponenten, wie z.B. verschiedene Alkalioxide, die wegen ihrer geringeren Bindungsstärke auch zu einer geringeren theoretischen Gesamtfestigkeit führen. Den größten festigkeitsmindernden Einfluss haben jedoch die Oberflächendefekte, deren Kerbwirkung die Ursache dafür ist, dass bei Biegeversuchen an nicht vorgespannten Flachgläsern nur 0,5 … 1 % der theoretischen Zugfestigkeit erreicht werden.
GRIFFITH verwendete zur mathematischen Lösung des Rissproblems das Prinzip vom Minimum der potentiellen Energie. Seine Bilanzierung beruht auf der Annahme, dass bei einer Rissvergrößerung (potentielle) elastische Energie freigesetzt wird, während die Bildung neuer Rissflanken im Gegenzug einen Anstieg der (potentiellen) Oberflächenenergie bewirkt. Hieraus lässt sich eine kritische Zugspannung sc ableiten, die senkrecht zu den Rissflanken wirkt und deren Überschreitung zum Bruch führt. Zudem kann eine Bruchzähigkeit KI.c (auch: kritischer Spannungsintensitätsfaktor) definiert werden. Sie ist ein Maß für die Energie, welche in der Umgebung der Rissspitze gespeichert ist und beschreibt den Widerstand gegen Risswachstum in reaktionsunfähiger (inerter) Umgebung.
Gl. 2![]()
mit:
sc … kritische Zugspannung senkrecht zu den Rissflanken,
E’ … ebener Spannungszustand = E, ebener Verzerrungszustand = E / (1 – m2),
a … Risslänge bzw. Risstiefe
Gl. 2.1
![]()
mit:
KI.c … Bruchzähigkeit
Die theoretische Bruchzähigkeit KI.c hängt nach Gl. 2 jedoch von der spezifischen Oberflächenenergie g0 ab, die in der Literatur meist als unterer Grenzwert angegeben ist. Deshalb wird die Bruchzähigkeit mit der eben beschriebenen Formel meist deutlich unterschätzt. Die Verwendung einer experimentell an genormten Proben ermittelten Bruchzähigkeit ist daher sinnvoll. Die folgende Tabelle gibt hierfür einige Ergebnisse an.
| Autor | Quelle | KI.c [MN∙m-3/2] |
| Wiederhorn | 1970, [5] | 0,82 |
| Gehrke, Ullner, Hähnert | 1988, [6] | 0,78 |
| Ullner | 1993, [7] | 0,76 |
Tab. 1: Bruchzähigkeiten von Kalk-Natron-Silicatglas
Um feststellen zu können, ob unter einer Zugspannung s ein Risswachstum zu erwarten ist, muss eine Vergleichsgröße zur Bruchzähigkeit definiert werden. Dies ist ein Spannungsintensitätsfaktor, welcher vor allem von der anliegenden Zugspannung selbst, aber auch von der Risstiefe und einem Kerbgeometriefaktor f abhängt, der die Charakteristik des Oberflächenschadens berücksichtigt.
Gl. 3
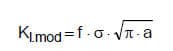
mit:
KI.mod … Spannungsintensitätsfaktor (Index „mod“, wegen Berücksichtigung von f),
f … Kerbgeometriefaktor (siehe Tab. 2),
s … senkrecht zu den Rissflanken einwirkende Zugspannung,
a .. Risslänge bzw. Risstiefe
| Schwächungsart | f [-] |
| Reibungsschwächung (Glas auf Glas) | 1,00 |
| Vickerseindruck (pyramidenförmiger Eindruck) | 1,18 |
| Schleifpapierschwächung | 1,77 |
| einfacher makroskopischer Oberflächenriss | 1,99 |
Tab. 2: Kerbgeometriefaktor f nach [7, 8]
Ein Bruch in inerter Umgebung ist nicht zu erwarten, wenn:
Gl. 4: Bruchkriterium
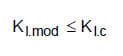
eingehalten ist.
Langzeitfestigkeit von nicht vorgespannten Glasprodukten
Die bisherigen bruchmechanischen Betrachtungen des vorherigen Kapitels taugen nur zur Bestimmung der Kurzzeitfestigkeiten von fabrikneuem Flachglas oder zur Bestimmung von Dauerfestigkeiten in inerter Umgebung. Keine Berücksichtigung fand bisher das so genannte subkritische bzw. unterkritische Risswachstum, welches bei Glas vor allem vom umgebenden Medium abhängt. Es begründet sich auf chemische Prozesse an der Risswurzel, die bei unter Zug beanspruchtem Glas ein stetiges Risswachstum bewirken, obwohl die spezifische Bruchzähigkeit KI.c, die beim GRIFFITH-Riss maßgeblich das Bruchkriterium bestimmt, noch nicht erreicht ist. Dieser langsame Rissfortschritt unterhalb der Bruchzähigkeit vermindert die Dauerfestigkeit gegenüber der Festigkeit des fabrikneuen Glases erheblich. Die Zugfestigkeit von Glas wird zu einer zeitabhängigen Kenngröße.
Durch die experimentelle Aufnahme der Risswachstumsgeschwindigkeit in Abhängigkeit des Spannungsintensitätsfaktors und des umgebenden Mediums lässt sich das sogenannte Potenzgesetz ableiten:
Gl. 5![]()
mit:
u … Risswachstumsgeschwindigkeit;
A, n … Risswachstumsparameter (nach Tab. 3);
KI.mod … Spannungsintensitätsfaktor.
KERKHOF, RICHTER und STAHN haben auf der Grundlage des empirisch hergeleiteten Potenzgesetzes eine Gleichung hergeleitet, mit der die Lebensdauer eines Glasbauteils unter konstanter, dauerhaft wirksamer Zugspannung abgeschätzt werden kann:
Gl. 6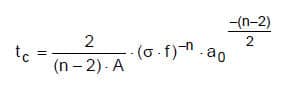
mit:
tc … prognostizierte Dauer bis zum Bruch;
A, n … Risswachstumsparameter nach Tab. 3;
s … konstante Dauerzugspannung;
f … Kerbgeometriefaktor nach Tab. 2;
a0 … Anfangsrisstiefe.
| umgebendes Medium | n [-] | A [m∙s-1]∙[MN-1∙m3/2] n |
| Wasser | 16,0 | 5,01 |
| Luft, 50% rel. Luftfeuchte | 18,1 | 0,447 |
| Vakuum | 70,0 | 250 |
Tab. 3: Unterkritisches Risswachstumsparameter von Kalk-Natron-Silicatglas bei Raumtemperatur [9, 10]
Eine weitere Rolle spielt die Beobachtung einer Rissfestsetzung. Bei einer vorhandenen Risstiefe, Umgebungsbedingung und Temperatur existiert demnach ein Schwellenwert der Zugspannung, unter welchem kein unterkritisches Risswachstum mehr zu erwarten ist. Es stellt sich offenbar ein Gleichgewichtszustand zwischen Rissheilungseffekten und der Rissausbreitung ein. Rissheilungseffekte an thermisch nicht vorgespannten Glasoberflächen können in lastfreien Zeitabschnitten zu einer Festigkeitserhöhung um bis zu 20 % (50 %) nach 4 Tagen (10 Tagen) im Vergleich zum vorgeschädigten Zustand [11, 12] führen. Die genauen Ursachen solcher Rissheilungen sind bisher unklar. Vermutlich spielt eine Ausrundung an der Risswurzel oder ein “Verkleben” der Rissufer durch Wasserstoffbrücken eine Rolle [13, Abschnitt 3.3.3.1]. Zur genauen Klärung der Ursachen sind in Zukunft noch intensivere Forschungen nötig. In Berechnungen bleibt die Rissheilung i.d.R. unberücksichtigt.
Fazit
Aus den dargelegten bruchmechanischen Zusammenhängen lassen sich drei wesentliche Aussagen für die Bemessung von nicht thermisch vorgespannten Gläsern ableiten:
1. Die Bruchwahrscheinlichkeit nimmt mit der Größe der zugbeanspruchten Oberfläche wegen der größeren Anzahl möglicher kritischer Risse zu. Hierbei ist die Verteilung der oberflächennahen Hauptzugspannungen zu berücksichtigen.
2. Der Bruch tritt i.d.R. nicht an der Stelle der maximalen Hauptzugspannung auf, sondern dort, wo zufällig ein relativ tiefer Oberflächenriss mit einer relativ großen Hauptzugspannung für eine kritische Kombination sorgt.
3. Die für den praktischen Einsatz von Flachgläsern entscheidende Dauerfestigkeit ist eine Funktion der Belastungsdauer und der Umgebungsbedingungen. Hierbei spielen die Temperatur und vor allem die Luftfeuchte eine Rolle. Es erscheint plausibel, dass der Bauteilwiderstand einer Glasschicht umso geringer ist, je länger die Einwirkungskombination den Riss geöffnet hält und das umgebende Medium dadurch chemische Reaktionen an der Risswurzel hervorrufen kann. In feuchter Umgebung oder bei hohen Temperaturen geht das unterkritische Risswachstum rascher voran und die Lebenszeit des Glasproduktes ist deshalb kürzer als bei Trockenheit oder niedrigen Temperaturen.
Quellenverzeichnis
[1] WÖRNER, J.-D.; SCHNEIDER, J.; FINK, A.: Glasbau – Grundlagen, Berechnung, Konstruktion. Berlin, Heidelberg: Springer-Verlag, 2001[2] GROSS, D.: Bruchmechanik. 2. Auflage, Berlin: Springer-Verlag, 1996
[3] PETZOLD, A.; MARUSCH, H.; SCHRAMM, B.: Der Baustoff Glas. 3. Auflage, Berlin: Verlag für Bauwesen, 1990
[4] HAHN, H.: Bruchmechanik – Einführung in die theoretischen Grundlagen. Stuttgart: T. G. Teubner, 1976
[5] WIEDERHORN, S. M.; BOLZ, L. H.: Stress corrosion and static fatique of glass. In: Journal of The American Ceramic Society, Vol. 53 (1970), No. 10, pp 543-548
[6] GEHRKE, E.; ULLNER, C.: Makroskopisches Rißwachstum, Inertfestigkeit und Ermüdungsverhalten silikatischer Gläser. Promotion, Technische Universität Berlin, 1988
[7] ULLNER, C.: Untersuchungen zum Festigkeitsverhalten von Kalk-Natronsilikatglas nach mechanischer Vorschädigung durch Korundberieselung. Berlin: BAM, 1993
[8] ULLNER, C.; HÖHNE, L.: Untersuchungen zum Festigkeitsverhalten und zur Rißalterung von Glas unter dem Einfluß korrosiver Umgebungsbedingungen. Berlin: BAM, 1993
[9] BLANK, K.: Dickenbemessung von vierseitig gelagerten rechteckigen Glasscheiben unter gleichförmiger Flächenlast. IKG-Forschungsbericht 3/93, 2. Auflage, Gelsenkirchen: Institut für Konstruktiven Glasbau, 1993
[10] SHEN, X.: Entwicklung eines Bemessungs- und Sicherheitskonzeptes für den Glasbau. Fortschritt-Berichte VDI, Reihe 4, Nr. 138, 1997
[11] FINK, A.: Ein Beitrag zum Einsatz von Floatglas als dauerhaft tragender Konstruktionswerkstoff. Dissertation. Institut für Statik, Technische Universität Darmstadt, 2000
[12] FINK, A.: Ein Beitrag zum Einsatz von Floatglas als dauerhaft tragender Konstruktionswerkstoff. Dissertation. Institut für Statik, Technische Universität Darmstadt, 2000
[13] SEDLACEK, G.; BLANK, K.; LAUFS, W.; GÜSGEN, J.: Glas im Konstruktiven Ingenieurbau. Berlin: Ernst & Sohn, 1999
Autor
Thomas Gröschke
M.Sc., Dipl.-Ing. (TU, FH)
TragWerk Software
Döking + Purtak Partnerschaft
![]() Artikel Bruchmechanik von Glas (Bauteilwiderstand) [ 176.65 KB ]
Artikel Bruchmechanik von Glas (Bauteilwiderstand) [ 176.65 KB ]

